ClimODE: Climate and Weather Forecasting With Physics-informed Neural ODEs

Oral (Top 1%), ICLR 2024
Yogesh Verma, Markus Heinonen, Vikas Garg
Aalto University, Finland & YaiYai Ltd
Paper Code arXiv

We model climate/weather as a spatiotemporal process using the concept of advection. This provides a strong physical prior to modeling the spatiotemporal dynamics. In order to model the external sources and provide uncertainty quantification, we add a Gaussian emission model , which models the day-night cycle and provides uncertainty quantification in the predictions. The video shows the predictions of the ClimODE model for various observables.

Abstract

Climate and weather prediction traditionally relies on complex numerical simulations of atmospheric physics. Deep learning approaches, such as transformers, have recently challenged the simulation paradigm with complex network forecasts. However, they often act as data-driven black-box models that neglect the underlying physics and lack uncertainty quantification. We address these limitations with ClimODE, a spatiotemporal continuous-time process that implements a key principle of advection from statistical mechanics , namely, weather changes due to a spatial movement of quantities over time. ClimODE models precise weather evolution with value-conserving dynamics, learning global weather transport as a neural flow, which also enables estimating the uncertainty in predictions . Our approach outperforms existing data-driven methods in global and regional forecasting with an order of magnitude smaller parameterization, establishing a new state of the art.

Overview

Method

How do we model weather/climate via advection?

Visualizations

Explore visualizations of how ClimODE models the global weather/climate.

Training Results

Results of ClimODE in various weather forecasting tasks.

Ablations

Ablations and Interpretability of Predictions

Method Overview

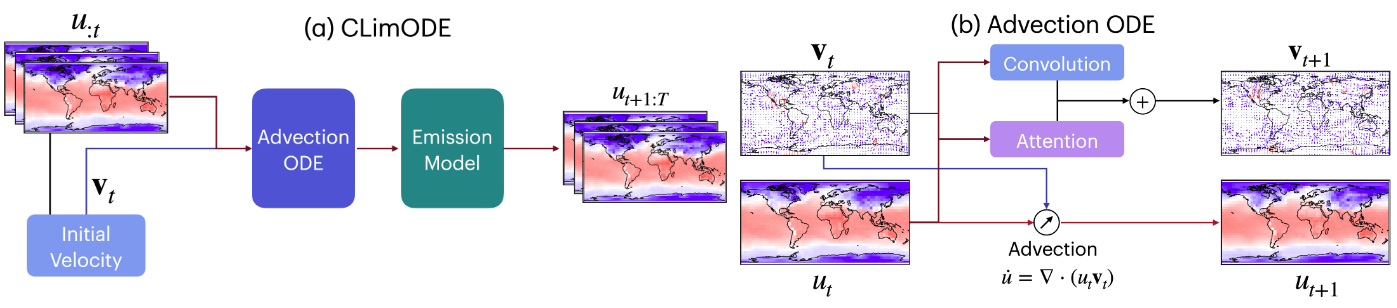
Our method whole pipeline. Based on initial velocity estimates, the advection ODE component serves as the foundational backbone of the model, projecting future predictions. These projections are subsequently forwarded to the emission model, further refining them by estimating bias and uncertainty, ultimately yielding the final predictions.

Neural Transport Model

We model weather/climate as a spatiotemporal process u(x,t) = (u1(x,t),...,uK(x,t)) of K quantities as an advection PDE,

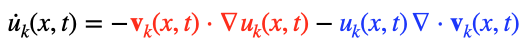
Flow velocity

We model the flow velocity by parametrising it as a function of u(t)= {u(x,t) : x ∈ Ω }, spatial gradients ∇ u(t), current velocity v(t) and spatiotemporal embeddings ψ as,

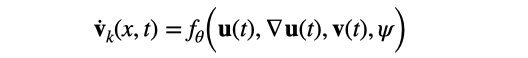
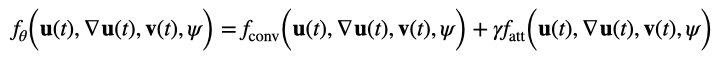
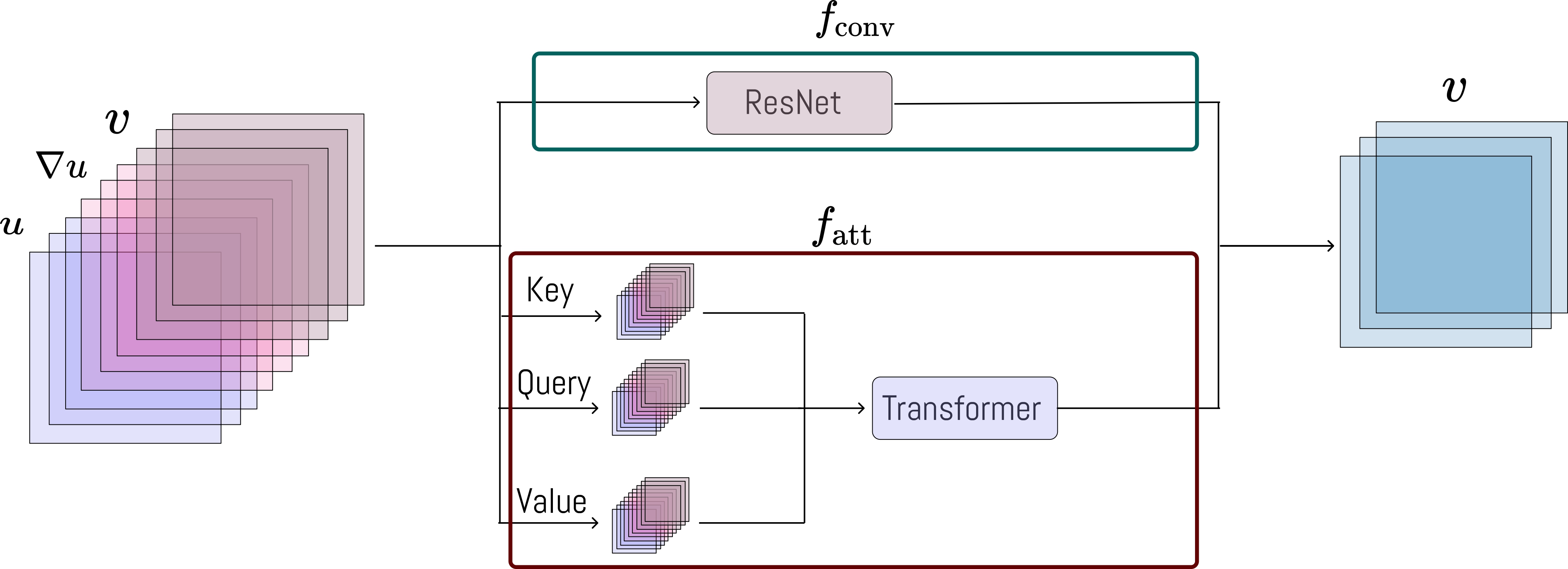
To capture local and global effects pertaining to weather (or climate), we propose a hybrid network as,



Results

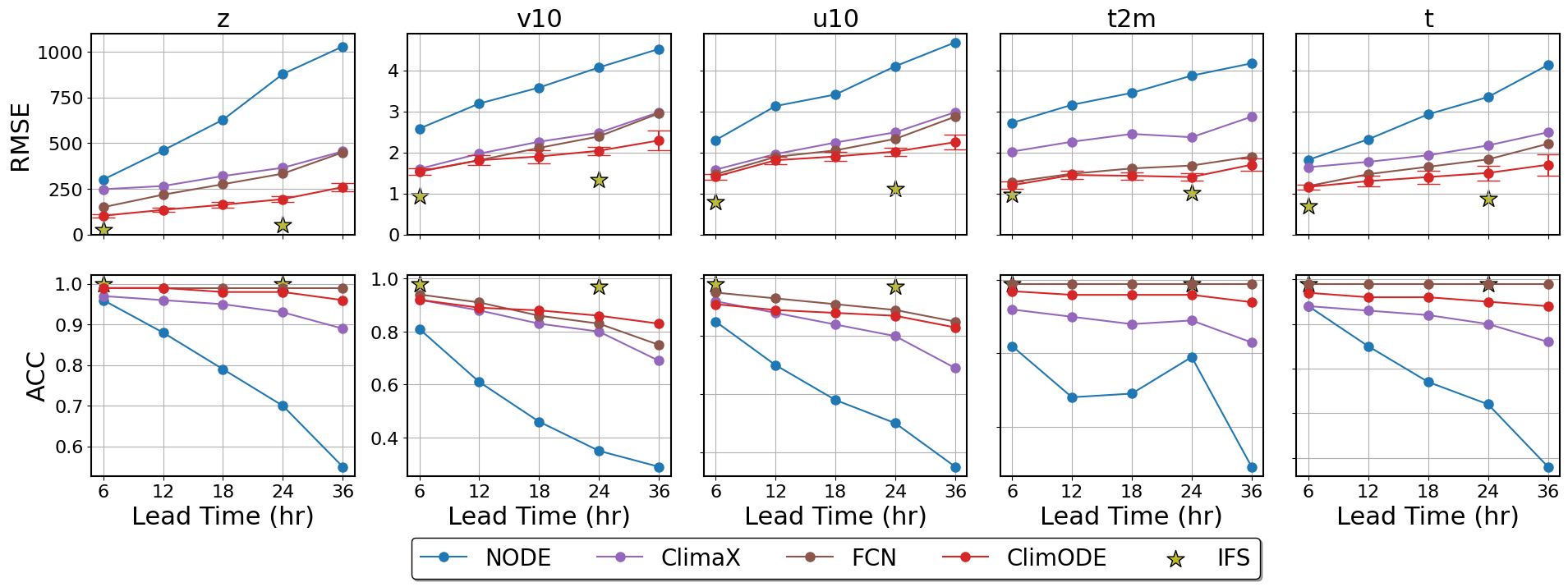
We now show the ClimODE's forecasting capabilities by predicting the future state based on the initial state for various lead times, focusing on key meteorological variables

Global Forecasting

We assess ClimODE's performance in global forecasting, encompassing the prediction of crucial meteorological variables described above. It demonstrates ClimODE's superior performance across all metrics and variables over other neural baselines, while falling short against the gold-standard IFS, as expected. These findings indicate the effectiveness of incorporating an underlying physical framework for climate or weather modeling.

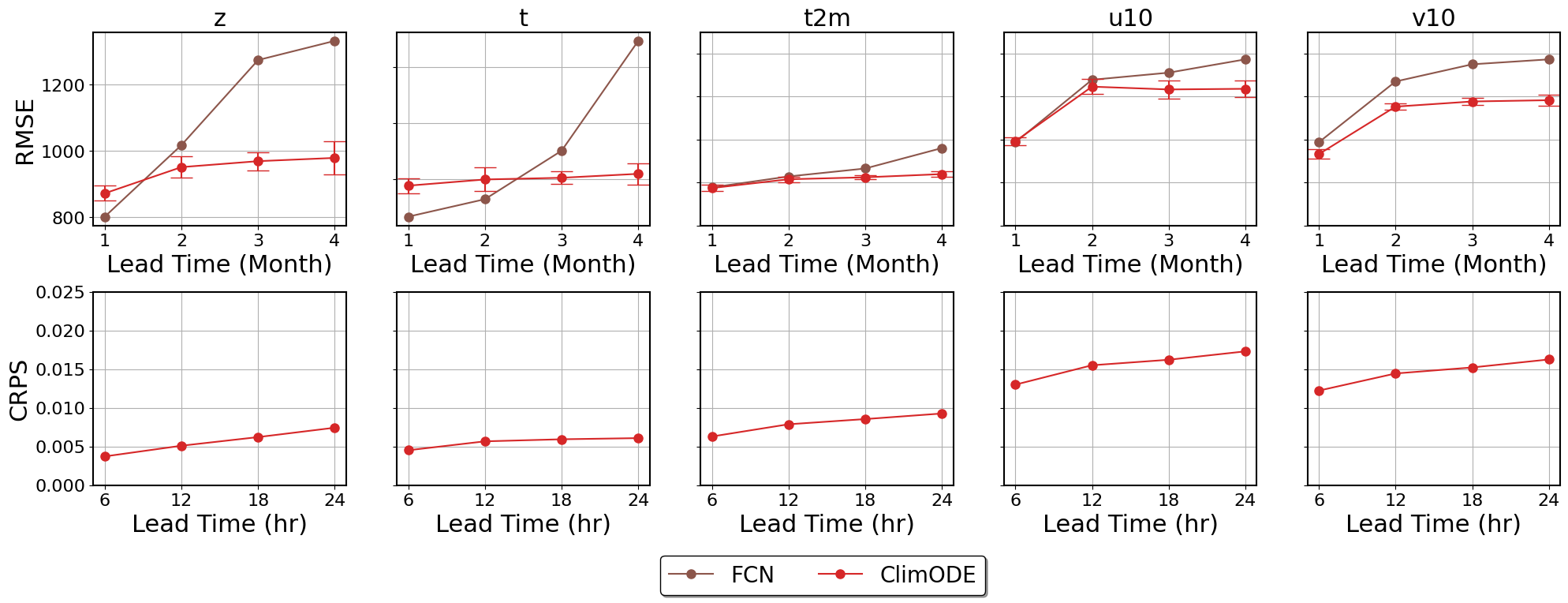
CRPS Scores and Monthly Forecasting

We also evaluated our model using CRPS (Continuous Ranked Probability Score) and Globaly monthly forecasting to forecast monthly averages of quantities, shown below. It can be seen our model can predict the weather quite well with predicted variance and bias outperform FCN in monthly forecasting.

Ablations

Effect of emission model

The right plot shows model predictions u(x,t) of ground temperature (t2m) for a specific location while also including emission bias µ and variance σ . Remarkably, the model captures diurnal variations and effectively estimates variance .

The bottom plot highlights bias and variance on a global scale. Positive bias is evident around the Pacific ocean , corresponding to daytime, while a negative bias prevails around Europe and Africa, signifying nighttime. The uncertainties indicate confidence in ocean estimation, with northern land regions being challenging.

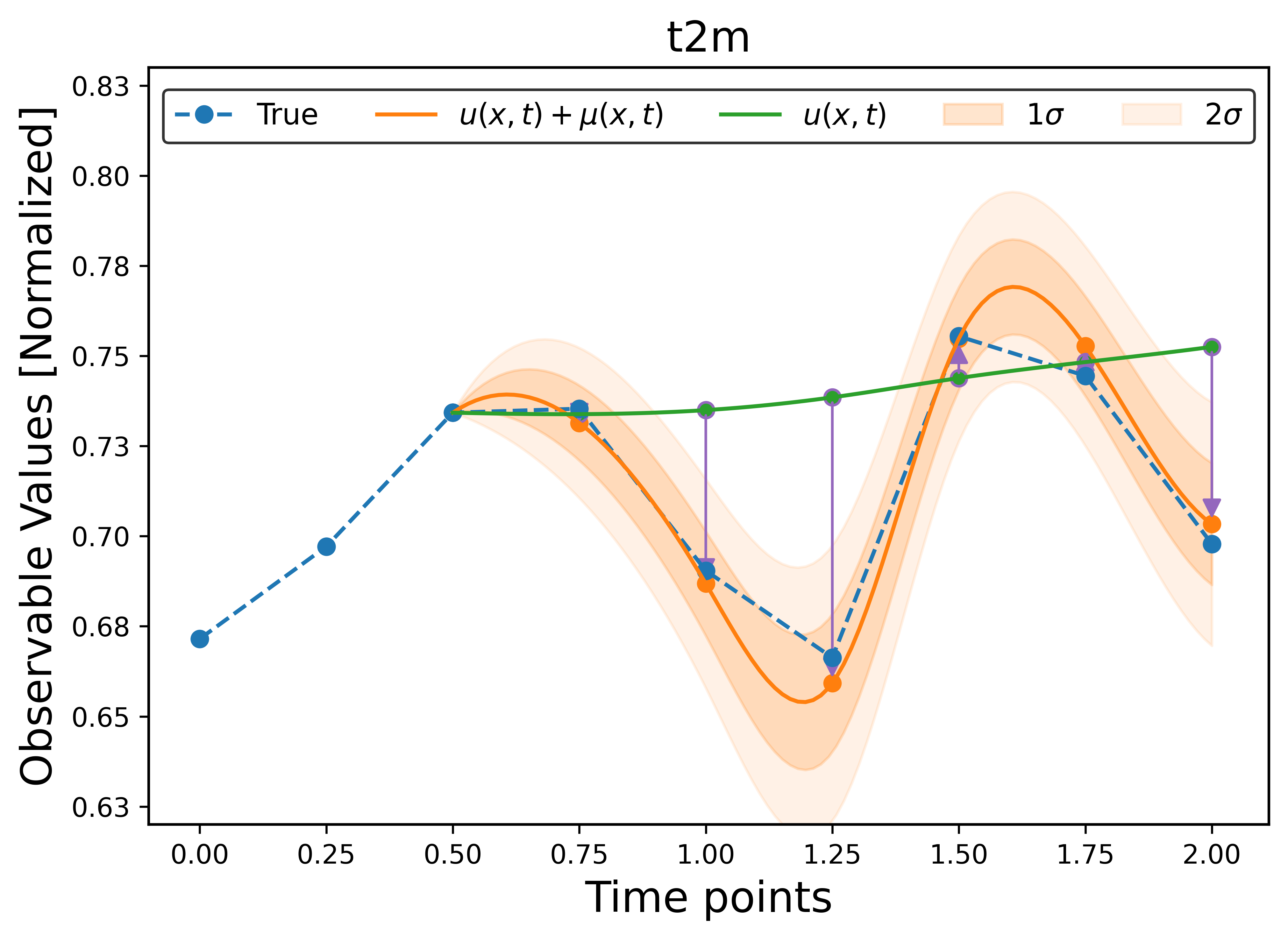
Agreement Score

Effect of individual components

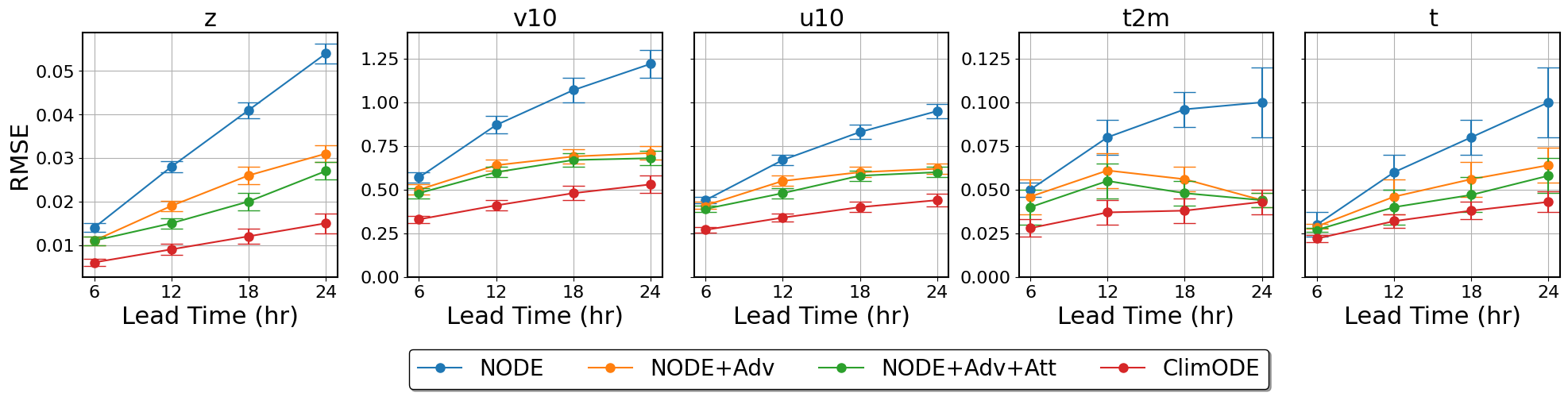
We analyze the contributions of various model components to its performance.The below plot delineates the impact of components: NODE is a free-form second-order neural ODE, Adv corresponds to the advection ODE form, Att adds the attention in addition to convolutions, and ClimODE adds also the emission component.

Additional results and analysis

We also have additional results on the following:

• Results for regional forecasting, longer-lead times of various quantities and comparison to baselines
• Abaltion to check the mass-conserving property of the ODE-system.
• Correlations among the data variables.

Visualizations

Global Predictions

Below is the global forecast video of various meteorological variables predicted by ClimODE.

Evolution by Advection

Below is the evolution of weather as a quantity-preserving advection system.

Poster

BibTeX

@inproceedings{
verma2024climode,
title={Clim{ODE}: Climate Forecasting With Physics-informed Neural {ODE}s},
author={Yogesh Verma and Markus Heinonen and Vikas Garg},
booktitle={The Twelfth International Conference on Learning Representations},
year={2024},
url={https://openreview.net/forum?id=xuY33XhEGR}
}