This website contains information regarding the paper AbODE: Ab Initio Antibody Design using Conjoined ODEs.
TL;DR: We propose a generative model for antibody design using conjoined interacting neural ODEs
Please cite our work if you find it useful:
@InProceedings{pmlr-v202-verma23a,
title = {\{A\}b\{ODE\}: Ab initio antibody design using conjoined {ODE}s},
author = {Verma, Yogesh and Heinonen, Markus and Garg, Vikas},
booktitle = {Proceedings of the 40th International Conference on Machine Learning},
pages = {35037--35050},
year = {2023},
editor = {Krause, Andreas and Brunskill, Emma and Cho, Kyunghyun and Engelhardt, Barbara and Sabato, Sivan and Scarlett, Jonathan},
volume = {202},
series = {Proceedings of Machine Learning Research},
month = {23--29 Jul},
publisher = {PMLR},
pdf = {https://proceedings.mlr.press/v202/verma23a/verma23a.pdf},
url = {https://proceedings.mlr.press/v202/verma23a.html}
}
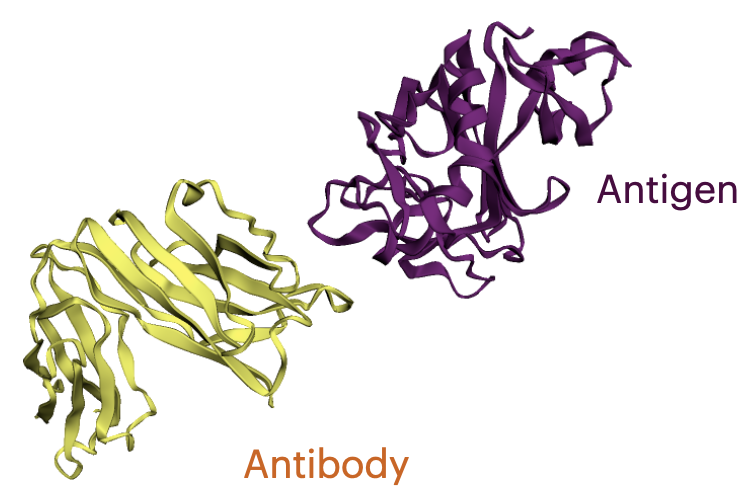
What is an Antibody?
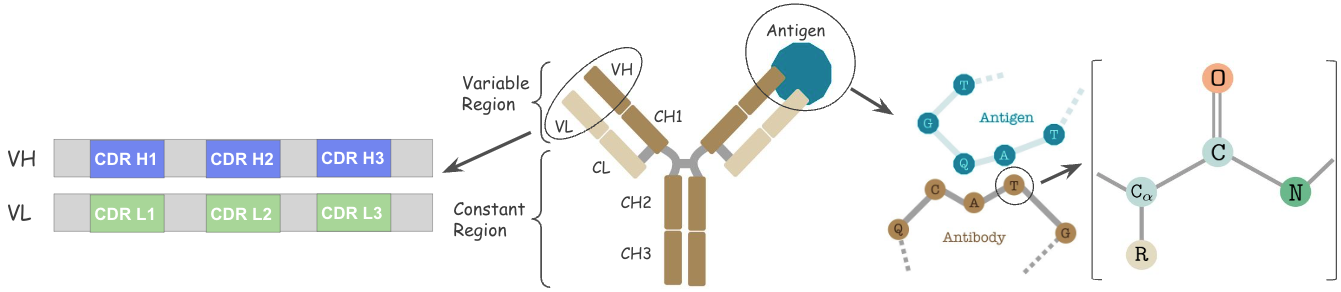
Antibodies are versatile proteins that bind to pathogens like viruses (Antigens) and stimulate a response. Each antibody recognizes a unique antigen, and the so-called Complementarity Determining Regions (CDRs) at the tip of the antibody determines this specificity.
Why model Antibody?
De novo generation of new antibodies targeting specific antigens is key to accelerating vaccine discovery. However, this co-design of the amino acid sequence and the 3D structure subsumes and accentuates some central challenges from multiple tasks, including protein folding (sequence to structure), inverse folding (structure to sequence), and docking (binding). Moreover, there is a combinatorial search space of over \(20^{L} +\) learning of joint distribution between Antibody and Antigen i.e. \(p(\texttt{Ab},\texttt{Ag})\).
Neural ODEs
Neural ODEs have been widely applied to graphs, such as GRAND, PDE-GCN, etc., providing a general way to create novel embedding methods. An ODE defines the dynamics of node updates as,
$$\dot{\mathbf{z}}_{i}(t) := \frac{\partial \mathbf{z}_i(t)}{\partial t} = f_\theta\big( t, \mathbf{z}_i(t), \mathbf{z}_{N_i}(t) \big), \qquad i = 1, \ldots, M$$
Where \(\mathbf{z}_{i}\) are node features, \(f_\theta\) is parametrized by a NN, and the model essentially learns a differential vector field that guides to create of expressive embeddings of nodes.
AbODE
Representation
We define antigen-antibody complex as a 3D graph \(G = (V,E,X)\), where \(V = (V_\mathrm{Ab},V_\mathrm{Ag})\), \(X = (X_\mathrm{Ab},X_\mathrm{Ag})\), \(E = (E_\mathrm{Ab},E_\mathrm{Ab-Ag})\), antibody \(\mathrm{Ab}\) and antigen \(\mathrm{Ag}\).
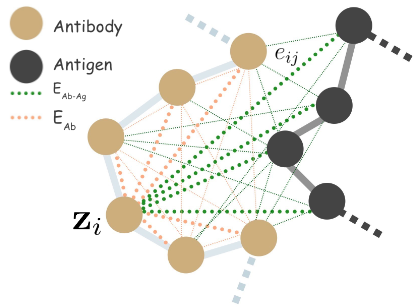
We define full connected heterogeneous edges between antibody \(E_\mathrm{Ab}\) residues, and \(E_\mathrm{Ab-Ag}\) antigen. Our node state is denoted by \(\mathbf{z}_i = [\mathbf{a}_i, \mathbf{s}_i]\), where \(\mathbf{a}_i \in \mathrm{R}^{20}\), a categorical distribution over the amino acid labels \(\{ \texttt{Arg},\texttt{His},\ldots \}\), and \(s_i\) is our novel quaternion type coordinate embedding.
Quaternion-type coordinate embedding
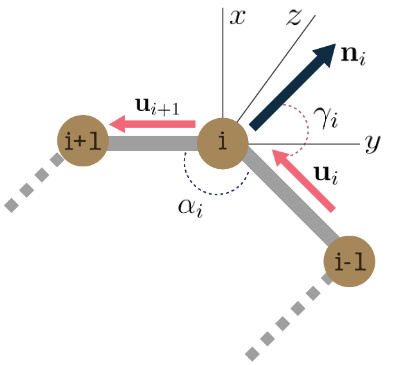
We also represent each residue by the cartesian 3D coordinates of its three backbone atoms \(\{ N, C_{\alpha}, C\}\). For the \(i^{th}\) residue \(\mathbf{x}_{i}\) we compute its spatial features \(\mathbf{s}_{i} = (r_{i},\alpha_{i},\gamma_{i})\), where, \(r_i\) denotes the distance between consecutive residues \(x_i\) and \(x_{i+1}\), \(\alpha_{i}\) is the co-angle of residue \(i\) wrt previous and next residue, \(\gamma_{i}\) is the azimuthal angle of \(i\)’s local plane, and \(\mathbf{n}_{i}\) is the normal vector. The full residue state \(\mathbf{z}_i = [\mathbf{a}_i, \mathbf{s}_i]\) concatenates the label features \(\mathbf{a}_i\) and the spatial features \(\mathbf{s}_i\) and \(\mathbf{u}_i = \mathbf{x}_{i+1} - \mathbf{x}_i\).
$$r_i = || \mathbf{u}_i ||, \quad \alpha_i = \cos^{-1}\left( \frac{\langle\mathbf{u}_i, \mathbf{u}_{i-1}\rangle}{||\mathbf{u}_i|| \cdot ||\mathbf{u}_{i-1}||}\right)$$
$$\gamma_i = \cos^{-1}\left( \frac{\langle \mathbf{u}_i , \mathbf{n}_i\rangle}{||\mathbf{u}_i|| \cdot ||\mathbf{n}_i||}\right), \quad \mathbf{n}_i = \mathbf{u}_i \times \mathbf{u}_{i-1}$$
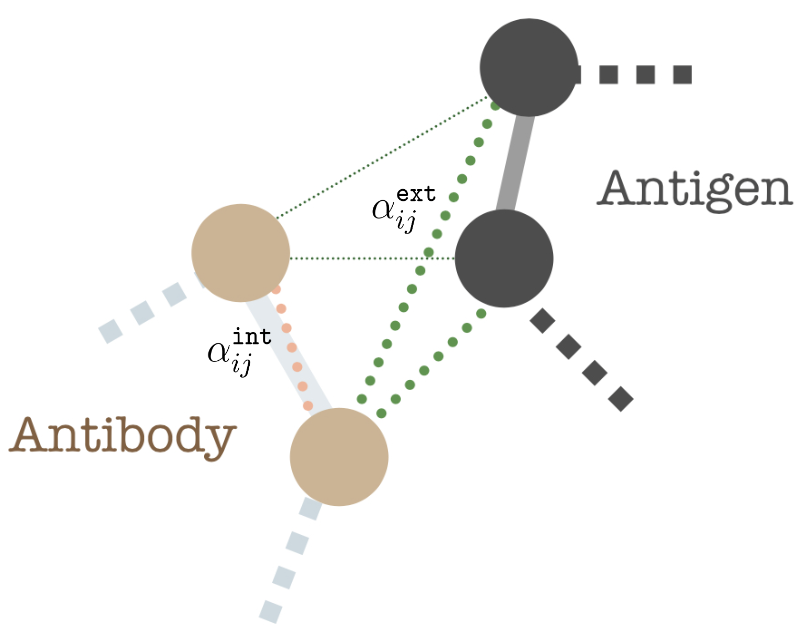
We model inter-antibody-antigen and intra-antibody interactions with a joint 3D graph over the antigen and the antibody using edge features,
$$ \mathbf{e}_{ij} = (\Delta \mathbf{z}_{ij}, i-j, \mathrm{RBF}(|| \mathbf{s}_i - \mathbf{s}_j|| ),O_{i}^{\top} \frac{s_{i,\alpha} - s_{j,\alpha}}{||s_{i,\alpha} - s_{j,\alpha} ||},~O_{i}^{\top}O_{j },~k_{ij} )$$
where state differences \(\Delta \mathbf{z}_{i j} = \{ \Delta \mathbf{a}_{ij}, \Delta \mathbf{s}_{ij}\}\), backbone distance \(i-j\), and spatial distance \(\texttt{RBF}(||\mathbf{s}_i-\mathbf{s}_j||)\) (here, RBF is the standard radius basis function kernel). The fourth term encodes directional embedding in the relative direction of \(j\) in the local coordinate frame \(O_i\). The \(O^{T}_i O_j\) describes the orientation encoding of the node \(i\) with node \(j\). Finally, we encode within-antibody edges with \(k = 1\) and antibody-antigen edges with \(k = 2\).
Conjoined System of ODEs
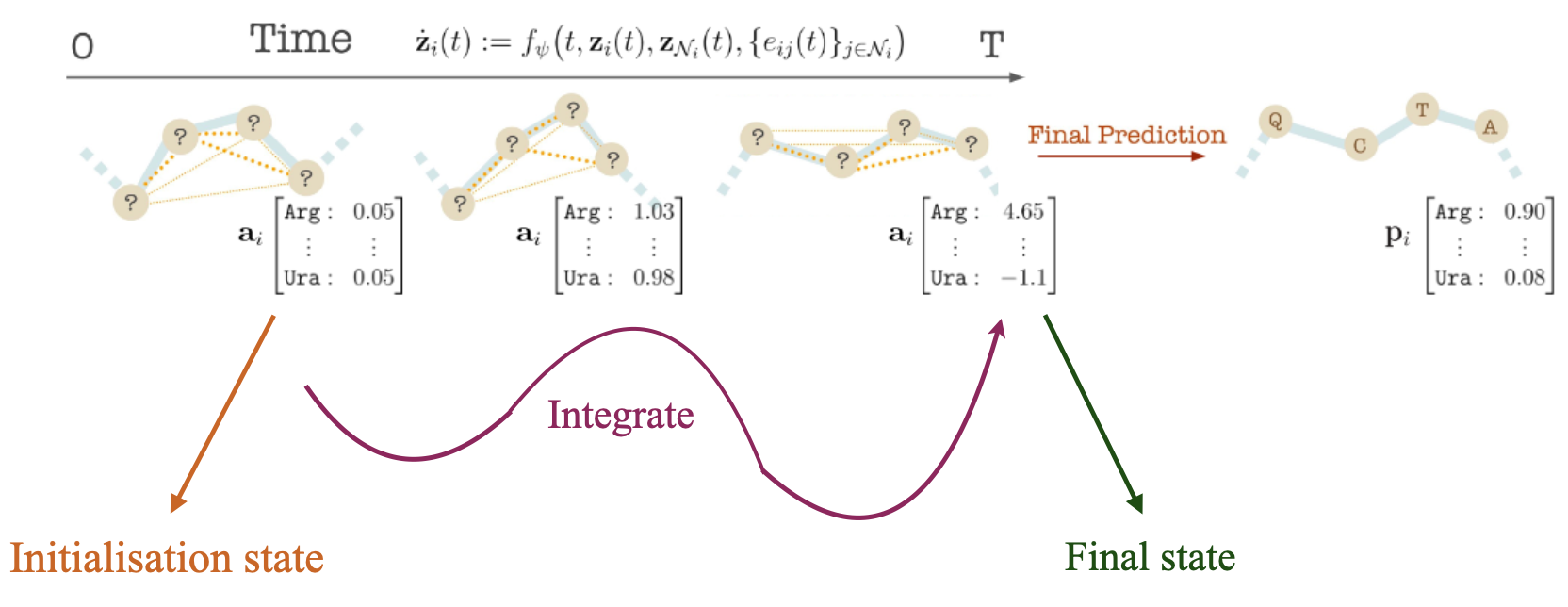
We model the distribution of antibody-antigen complexes by ODE over \(\mathbf{z}(t)\) over time \(t \in \mathrm{R}_{+}\). We initialize the initial state \(\mathbf{z}(0)\) to a uniform categorical vector and coordinates are initialized with the even distribution between the residue right before CDRs and the one right after CDRs, and we learn a differential \(\frac{d\mathbf{z}(t)}{dt}\) that maps to the end state \(\mathbf{z}(T)\) that matches data.
We begin by assuming an ODE system \(\{\mathbf{z}_{i}(t)\}\) over time \(t \in \mathrm{R}_{+}\), where node the time evolution of node \(i\) is an ODE
$$\dot{\mathbf{z}}_i(t) = \frac{\partial \mathbf{z}_i(t)}{\partial t} = f_\psi\big( t, \mathbf{z}_i(t), \mathbf{z}_{N(i)}(t), \{ \mathbf{e}_{ij}(t)\}_j \big)$$
Collecting all, we get a system of conjoined ODEs, which can be solved using ODEsolvers.
$$\dot{\mathbf{z}}(t) \triangleq \begin{pmatrix} \dot{\mathbf{z}}_1(t) \\ \vdots \\ \dot{\mathbf{z}}_M(t) \end{pmatrix} = \begin{pmatrix} f_\psi\big( t, \mathbf{z}_1(t), \mathbf{z}_{N(1)}(t), \{ \mathbf{e}_{1j}(t)\}_j \big) \\ \vdots \\ f_\psi\big( t, \mathbf{z}_M(t), \mathbf{z}_{N(M)}(t), \{ \mathbf{e}_{Mj}(t)\}_j \big) \end{pmatrix}$$
Attention-based Differential
We capture the interactions between the antigen and antibody residues with graph attention, as,
$$\alpha_{ij} = \texttt{softmax}\left( \frac{\left(\mathbf{W}_3 \mathbf{z}_i\right)^{\top}\left(\mathbf{W}_4 \mathbf{z}_j + \mathbf{W}_6 \mathbf{e}_{i j}\right)}{\sqrt{d}} \right)$$
$$\mathbf{z}_i^{\prime}= \mathbf{W}_1 \mathbf{z}_i + \sum_{j \in N_{int}(i)} \alpha_{ij}^{\texttt{int}}\left(\mathbf{W}_2 \mathbf{z}_j+\mathbf{W}_6 \mathbf{e}_{i j}\right) + \sum_{j \in N_{ext}(i)} \alpha_{ij}^{\texttt{ext}}\left(\mathbf{W}^{\prime}_2 \mathbf{z}_j+\mathbf{W}^{\prime}_6 \mathbf{e}_{i j}\right)$$
Training Objective
We optimize our model jointly with loss consisting of two components: one for the sequence and another for the structure, as,
$$L = L_\mathrm{seq} + L_\mathrm{structure}$$
where,
$$L_\mathrm{seq} = \frac{1}{N} \sum_{n=1}^{N} \frac{1}{M}\sum_{i=1}^{M_i} \mathrm{CE}(\mathbf{a}_{ni}^{\mathrm{true}}, \mathbf{a}_{ni} ) \quad L_{\mathrm{structure}} = -\frac{1}{N} \sum_{n=1}^N \frac{1}{M}\sum_{i=1}^{M_i} \lambda(L_{\mathrm{angle}}^{ni} + L_{\mathrm{radius}}^{ni})$$
The angle loss is defined using negative von-mises log-likelihood and radii loss using using negative gaussian log-likelihood as,
$$L_{\mathrm{angle}}^{ni} = \sum_k^{\{ \texttt{C}_{\alpha}, \texttt{C}, \texttt{N} \}} \sum_{\theta \in \{\alpha,\gamma\}} \log M(\theta_{ik}^{n} \mid \theta_{ik}^{n,true}, \kappa) \quad L_\mathrm{radius}^{ni} = \sum_{k}^{\{ \texttt{C}_{\alpha}, \texttt{C}, \texttt{N} \}} \log N( r_{ik}^{n} | r_{ik}^{n,true}, \sigma_r^2 )$$
Sequence and Structure Generation
Given the antibody or antigen-antibody complex, we generate an antibody sequence and the corresponding structure by solving the system of ODEs for time T to obtain \(\mathbf{z}(T ) = [\mathbf{a}(T), \mathbf{s}(T)]\). We transform the label features \(\mathbf{a}(T )\) into Categorical amino acid probabilities \(\textbf{p}\) using the softmax operator. We pick the most probable amino acid per node.
Results
Unconditioned Antibody Sequence and Structure Generation
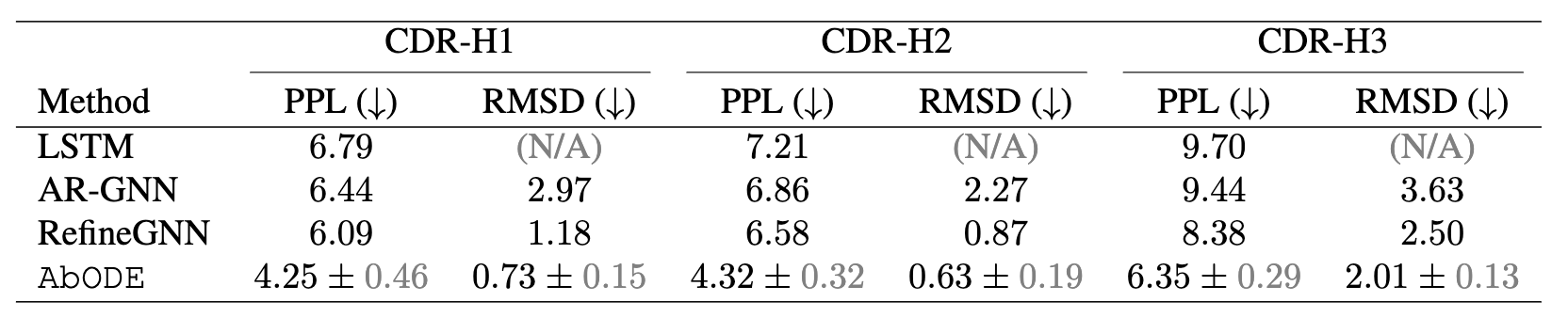
The task is to generate antibody sequence and structure without any external conditioning, where we used PPL : Perplexity (Exponential of negative log-likelihood) and RMSD: Root Mean Square Deviation by Kabsch Algorithm as our metrics.
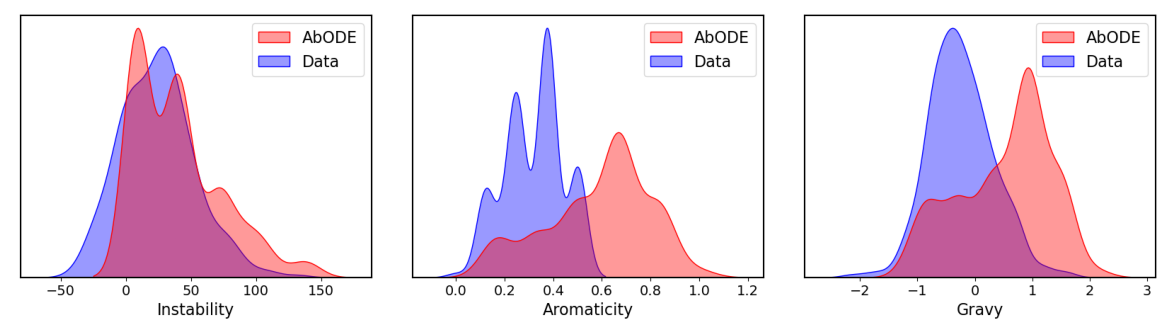
Some generated structures via \(\texttt{AbODE}\) are also shown above. We visually evaluate the generated structures via out method via properties distribution. We utilize kernel density estimation of these distributions to visualize these distributions. We use
- Gravy: The Gravy value is calculated by adding the hydropathy value for each residue and dividing it by the sequence length.
- Instability: The Instability index predicts regional instability of dipeptides that occur more frequently in unstable proteins when compared to stable proteins
- Aromaticity: It calculates the aromaticity value of a protein, which is simply the relative frequency of Phe+Trp+Tyr
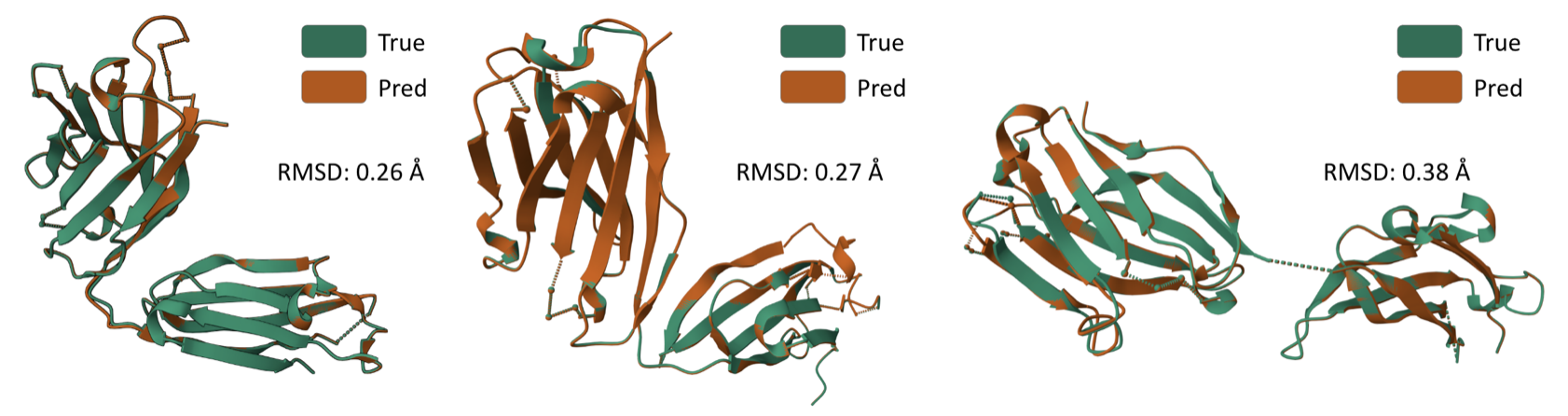
Conditioned Antibody Sequence and Structure Generation
The task is to generate antibody sequence and structure with an external conditioning i.e. the Antigen, where we used AAR: Amino Acid Recovery rate, defined as the overlapping rate between the predicted 1D sequences and the ground truth and RMSD as our metrics.

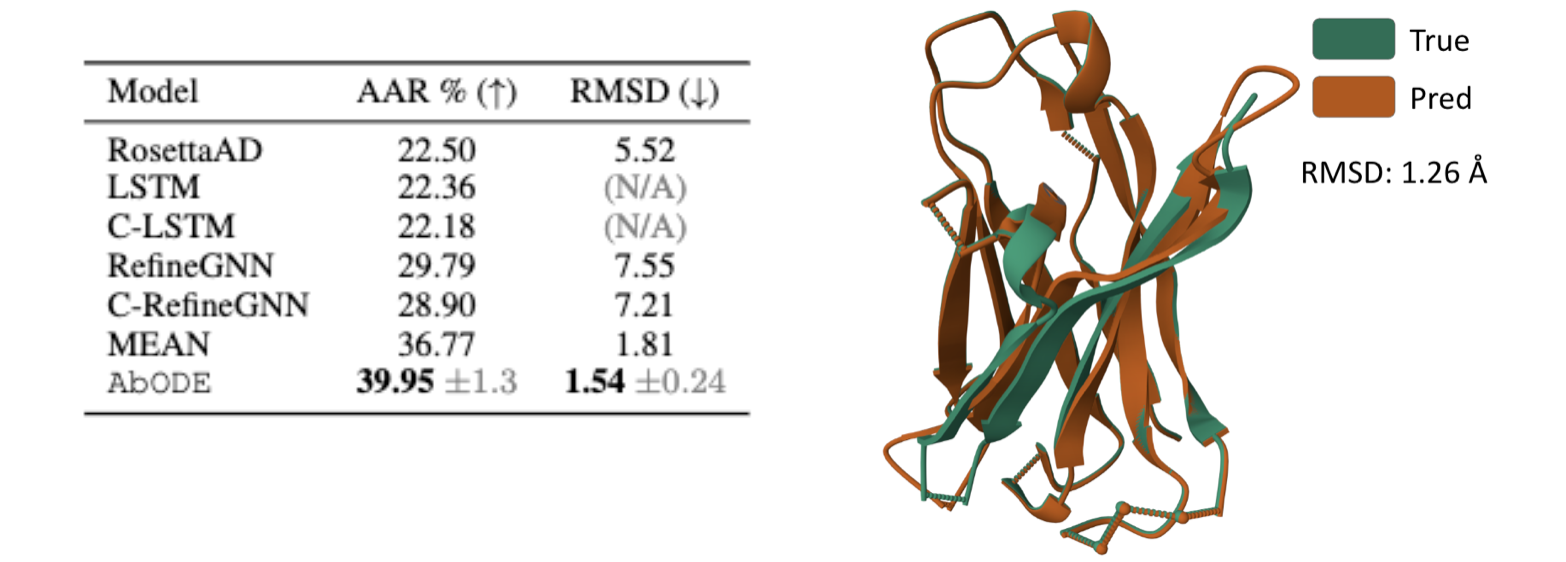
Antigen-binding CDR-H3 Design
Design CDR-H3 that binds to a given antigen, evaluated on 60 diverse complexes selected by RabD
Conclusion
- We propose AbODE, which models the antibody-antigen complex as a joint graph, and via a system of coupled residue-specific ODEs.
- AbODE can incorporate conditional contextual and spatial information in ODEs tailored for Antibody design.
References
- Iterative refinement graph neural network for antibody sequence-structure co-design, Jin et al., ICLR 2022
- Independent SE(3)-Equivariant Models for End-to-End Rigid Docking, Ganea et al., ICLR 2022
- Modular Flows: DIfferential Molecular Generation, Verma et al., NeurIPS 2022
- Conditional Antibody Design as 3D Equivariant Graph Translation, Kong et al., ICLR 2023
- Generative Models for Graph-based Protein Design, Ingraham et al., NeurIPS 2019
- Neural Ordinary Differential Equations, Chen et al., NeurIPS 2018